I I. ДИАЛОГ О СЛУЧАЕ и ТЕОРИИ ВЕРОЯТНОСТИ
А. - Теория вероятностей, быть может, одна
из самых замечательных наук; Лаплас называл ее даже самой замечательной
(1). Но у нее есть странные особенности. Одна из них заключается
в том, что нет вполне удовлетворительных определений ее основных понятий,
- по крайней мере определений философских. По существу ведь «случай» (как
и «вероятность») основное понятие этой науки. Паскаль, один из главных
ее создателей, назвал ее «геометрией случая». Напрасно было бы, однако,
искать точного определения этого понятия в трудах ее классиков; по крайней
мере, я такого не нашел ни у Паскаля, ни у Кондорсе, ни у Лапласа, ни даже
(это говорю с ограничением) у Курно. Чебышев в своей замечательной по глубине
работе (2), почему-то иногда замалчиваемой точно умышленно (3),
не произносит слова «случай». Очень плохие определения этого понятия есть
у философов, никогда теорией вероятностей не занимавшихся. «Мы называем
случайными такие события, неожиданное свершение которых представляется
нам самопроизвольным («spontan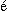 »)
и как бы излишним, т. е. не вызванным настоятельной необходимостью», -
говорит Ридингер (4). «Факты, которые мы не можем связать посредством
причинности с другими точно определенными фактами, вызывают у нас ощущение
случая», - говорит де Монтессю (5). Случайность «везде нарушает
закон вещей, преобладающее, правильное», - говорит Адольф Лассон (6).
Даже по форме это не определения. А по существу они, конечно, не определяют
ровно ничего. Что такое «самопроизвольность» в событиях? Какие события
надо считать вызванными именно настоятельной необходимостью? Как следует
понимать «закон вещей»? Названные авторы пытаются определить неясное понятие
понятиями еще более неясными. К тому же, если мы сегодня не можем связать
двух событий между собой, то, быть может, это будет сделано завтра: случай
не может быть понятием временным. Если же такую возможность предположить,
то очень легко прийти к полному отрицанию случая. Многие ученые, не желающие
отступать от абсолютного детерминизма (который, как им кажется, подрывается
идеей случая), действительно случай и отрицают. Лаплас и Кетле, независимо
один от другого, высказали почти в одних и тех же словах мысль: «Случай
есть только псевдоним незнания». В действительности это изречение принадлежит
Боссюэту: «Не будем больше говорить ни о случае, ни о счастье (Fortune),
или же будем о них говорить как о названии, которым мы прикрываем наше
невежество. То, что есть случай для нашего слабого (incertain) суждения,
есть принятое намерение в совете высшем, в том вечном совете, куда входят
в одном порядке все причины и все следствия» (7). Перевожу опять
очень нехорошо, нет ничего труднее, чем переводить Боссюэта. Но мысль я
передаю во всяком случае правильно, и это, вероятно, единственное, в чем
Боссюэт сходится с многими материалистами. В теории вероятностей есть одно
уравнение, называющееся formule du hasard, но в философском смысле оно
ничего не дает. Из математиков лучше других определил случай Пуассон: «Под
случаем (hasard) надо разуметь совокупность причин, способствующих осуществлению
события и не оказывающих влияния на размер его вероятности,
»)
и как бы излишним, т. е. не вызванным настоятельной необходимостью», -
говорит Ридингер (4). «Факты, которые мы не можем связать посредством
причинности с другими точно определенными фактами, вызывают у нас ощущение
случая», - говорит де Монтессю (5). Случайность «везде нарушает
закон вещей, преобладающее, правильное», - говорит Адольф Лассон (6).
Даже по форме это не определения. А по существу они, конечно, не определяют
ровно ничего. Что такое «самопроизвольность» в событиях? Какие события
надо считать вызванными именно настоятельной необходимостью? Как следует
понимать «закон вещей»? Названные авторы пытаются определить неясное понятие
понятиями еще более неясными. К тому же, если мы сегодня не можем связать
двух событий между собой, то, быть может, это будет сделано завтра: случай
не может быть понятием временным. Если же такую возможность предположить,
то очень легко прийти к полному отрицанию случая. Многие ученые, не желающие
отступать от абсолютного детерминизма (который, как им кажется, подрывается
идеей случая), действительно случай и отрицают. Лаплас и Кетле, независимо
один от другого, высказали почти в одних и тех же словах мысль: «Случай
есть только псевдоним незнания». В действительности это изречение принадлежит
Боссюэту: «Не будем больше говорить ни о случае, ни о счастье (Fortune),
или же будем о них говорить как о названии, которым мы прикрываем наше
невежество. То, что есть случай для нашего слабого (incertain) суждения,
есть принятое намерение в совете высшем, в том вечном совете, куда входят
в одном порядке все причины и все следствия» (7). Перевожу опять
очень нехорошо, нет ничего труднее, чем переводить Боссюэта. Но мысль я
передаю во всяком случае правильно, и это, вероятно, единственное, в чем
Боссюэт сходится с многими материалистами. В теории вероятностей есть одно
уравнение, называющееся formule du hasard, но в философском смысле оно
ничего не дает. Из математиков лучше других определил случай Пуассон: «Под
случаем (hasard) надо разуметь совокупность причин, способствующих осуществлению
события и не оказывающих влияния на размер его вероятности,
т. е. на отношение числа случаев (cas), благоприятных его осуществлению,
к общему числу возможных случаев» (8). По необходимости употребляю
одно слово «случай» для перевода французских слов «hasard» и «cas». Это
определение тоже не может быть названо удовлетворительным, так как оно
у Пуассона, в связи с его общим пониманием причинности, устанавливает какое-то
различие между «настоящими» причинами явления и причинами, которые только
«способствуют» (concourent) его осуществлению. Многие определения случая
основаны на неправильном разделении между «известными и постоянными факторами
события» и «факторами неизвестными, меняющимися». Чубер и называет первые
«причинами», а вторые «случаем» (9). Между тем «известность» и «неизвестность»
опять-таки всегда имеют лишь временный характер; а «постоянство» никакой
роли тут не играет: солнце встает и заходит каждый день, тогда как землетрясения
или извержения вулканов бывают непостоянно; однако, у нас не больше оснований
считать извержения и землетрясения явлением «случайным», чем считать таким
явлением восход и заход солнца. Поэтому и определения Чубера я никак принять
не могу. В сущности близок к его позиции и Мах, рассматривающий случай,
как «скрытую правильность» и сводящий его к «обстоятельствам, которые нам
неизвестны, и на которые мы не можем оказать влияния» (10).
Л. - Я предпочел бы узнать то, что думали о
случае классики новейшей философии. Если не ошибаюсь, Кант употребляет
это слово лишь в бытовом, повседневном смысле. Но, быть может, я ошибаюсь:
я не читал всего Канта, как не прочел всего, даже всего главного,
из книг других классиков.
А. - Всего у всех классиков философии
не прочла, верно, и одна десятая специалистов. О себе я мог бы сказать
разве лишь то, что у Декарта я прочел всe, a «Discours de la Methode» читал
не один раз, читал так, как именно Кант советовал читать шедевры. Он где-то
пишет: «Я должен так долго читать Руссо, чтобы меня перестала беспокоить
красота выражения, и чтобы я мог рассматривать его прежде всего разумом»,
К этому Кант - весьма, по-моему, для него неожиданно - добавляет: «Великие
люди блестят лишь на расстоянии, и князь много теряет в глазах своего лакея.
Это происходит оттого, что великих людей нет» (11). В отношении
Канта вы тут не вполне правы: Кант кое-где говорит о случае, о Zufall,
и, чаще, о Zuf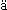 lligkeit (12).
Но он стоит на классическом, предшествовавшем Курно, противопоставлении
случая и причинности, хотя занимает тут не крайнюю (Боссюэто-Лапласовскую)
позицию: «Принцип: ничто не происходит в силу слепого случая (in mundo
non datur casus) есть априорный закон природы. То же самое относится к
другому принципу: в природе нет слепой необходимости, но есть необходимость
условная (non datur fatum)», говорит он (13). Кант дает и определение
случая, но чисто отрицательное и беспредельно общее: «Etwas dessen Nichtsein
sich denken l
lligkeit (12).
Но он стоит на классическом, предшествовавшем Курно, противопоставлении
случая и причинности, хотя занимает тут не крайнюю (Боссюэто-Лапласовскую)
позицию: «Принцип: ничто не происходит в силу слепого случая (in mundo
non datur casus) есть априорный закон природы. То же самое относится к
другому принципу: в природе нет слепой необходимости, но есть необходимость
условная (non datur fatum)», говорит он (13). Кант дает и определение
случая, но чисто отрицательное и беспредельно общее: «Etwas dessen Nichtsein
sich denken l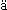 sst» (14).
Но вы правы в том смысле, что и у него, как и у других классиков новой
философии, идея случая почти не занимает места в системе.
sst» (14).
Но вы правы в том смысле, что и у него, как и у других классиков новой
философии, идея случая почти не занимает места в системе.
Л. - Вам остается только дать ваше собственное
определение случая.
А. - Для ясности спора я очень «заострю» свой
ответ, в надежде, что вы сделаете поправку на заострение. Случай есть все,
что происходит в мире, его возникновение, создание планеты Земля, появление
человечества на этой планете, его возможное в будущем исчезновение, рождение
человека, его смерть, бесконечная совокупность больших, средних, малых
явлений, все что «по законам природы» происходит во Вселенной, то, что
Кант называет совокупностью всех фактов, «die absolute Totalit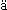 t
des Iribegriffs existierender Dinge». С моей точки зрения, историю человечества,
с разными отступлениями и падениями, можно представить себе как сознательную
или бессознательную, героическую или повседневную, борьбу со случаем. Однако,
ходячие слова «не оставлять ничего на волю случая», «ne laisser rien au
hasard», представляются мне предельным выражением человеческого высокомерия
и легкомыслия.
t
des Iribegriffs existierender Dinge». С моей точки зрения, историю человечества,
с разными отступлениями и падениями, можно представить себе как сознательную
или бессознательную, героическую или повседневную, борьбу со случаем. Однако,
ходячие слова «не оставлять ничего на волю случая», «ne laisser rien au
hasard», представляются мне предельным выражением человеческого высокомерия
и легкомыслия.
Л. - Нелюбезный и недоверчивый человек, вероятно,
в ваших словах увидел бы сознательное или бессознательное желание  pater
le bourgeois. Они вдобавок и противоречивы. Если всё случай, то
какая же может быть с ним «борьба»? А если борьба возможна, то «предельное
выражение человеческого высокомерия и легкомыслия» есть лишь ее удачная,
победоносная форма. Впрочем, я думаю, что вы к этому вернетесь и пока лишь
слишком «заострили» вашу мысль? Вы и говорите так, точно пишете слово «случаи»
с большой буквы. В очень далекие времена понятия «случай», «судьба» чрезвычайно
занимали людей. У греков для них было пять или даже, кажется, шесть слов,
означавших одно и то же или, собственно, почти ничего не означавших. Много
говорилось о судьбе и в Средние века. Но чем культурнее становился мир,
чем дальше шли наука и философия, тем меньше места уделялось этим медленно
умирающим понятиям. Во всяком случае, никто никогда не толковал историю
человечества, как процесс борьбы со случаем, и никто не связывал случай
с законами природы. Может быть, я сегодня умру от удара или меня кто-нибудь
убьет, - это будет, если хотите, случай. Но то, что я рано или поздно умру
непременно, - это уже не случай, а закон природы, очень для нас печальный.
pater
le bourgeois. Они вдобавок и противоречивы. Если всё случай, то
какая же может быть с ним «борьба»? А если борьба возможна, то «предельное
выражение человеческого высокомерия и легкомыслия» есть лишь ее удачная,
победоносная форма. Впрочем, я думаю, что вы к этому вернетесь и пока лишь
слишком «заострили» вашу мысль? Вы и говорите так, точно пишете слово «случаи»
с большой буквы. В очень далекие времена понятия «случай», «судьба» чрезвычайно
занимали людей. У греков для них было пять или даже, кажется, шесть слов,
означавших одно и то же или, собственно, почти ничего не означавших. Много
говорилось о судьбе и в Средние века. Но чем культурнее становился мир,
чем дальше шли наука и философия, тем меньше места уделялось этим медленно
умирающим понятиям. Во всяком случае, никто никогда не толковал историю
человечества, как процесс борьбы со случаем, и никто не связывал случай
с законами природы. Может быть, я сегодня умру от удара или меня кто-нибудь
убьет, - это будет, если хотите, случай. Но то, что я рано или поздно умру
непременно, - это уже не случай, а закон природы, очень для нас печальный.
А. - Вы здесь только передвигаете случай в
пространстве и во времени. Я действительно считаю нужным различить случай
непосредственный
и случай отдаленный. В чисто-случайном многотысячелетнем процессе
космического и биологического развития вышло так, что человек живет лет
60-80, слон гораздо больше, а собака гораздо меньше. К тому же человек
будто бы когда-то жил и дольше. Мафусаил дожил до 969 лет, и Мечников,
предполагая, вместе с Гензелером, что в те времена под годом разумелся
сезон, считал возможным, что Мафусаилу в момент смерти было 242 года (15),
- возраст тоже довольно почтенный... Что же касается «законов природы»,
то они и представляют собой попытку борьбы со случаем в области научно-познавательной.
Они - первые, вторые, третьи приближения к тому, что называется научной
истиной; а какое будет десятое приближение - неизвестно. Теперь многие
физики и химики, как вы знаете, склонны считать законы природы некоторым
подобием статистических обобщений. В предельно заостренной форме выражают
это Джине и Борель: нельзя считать невозможным, что вода, поставленная
на огонь вместо того, чтобы закипеть, замерзнет; это лишь чрезвычайно маловероятно
(16). У других физиков такой взгляд не вполне удовлетворяет «потребность
причинности», и они предпочли бы считать подобную интерпретацию законов
природы лишь временной. Мизес справедливо называет их взгляд «предрассудком»
(17). Да, собственно говоря, нет и ничего особенно нового в идее
статистического подхода к законам природы. Сходный взгляд высказывал еще
Лаплас. «Строго говоря, - писал он, - можно даже сказать, что почти все
наши знания только вероятны, а в небольшом числе вещей, которые мы можем
знать достоверно, в самих математических науках, главные средства для достижения
истины, индукция и аналогия, основываются на вероятности». Говорил так
детерминист из детерминистов, типичнейший мыслитель 18-го столетия с его
безграничной верой в разум. В сущности, в настоящее время закон природы
может быть в общей форме выражен лишь следующим образом: в таком-то кругу
явлений, при таких-то аксиомах и обозначениях, связь таких-то величин почти
всегда может быть выражена такой-то приблизительной математической
формулой. В древности безграничной веры в разум не было и быть не могло.
Перед ранними исследователями природы было то, что непосредственно последовало
за первозданным хаосом. К нему надо было как-то подойти, за что-то ухватиться.
У греков мифология приукрасила хаос и сделала его богом. По Гезиоду, рядом
с Хаосом было нечто много худшее. Тартар, и нечто много лучшее, Любовь.
Между ними шла борьба. По иному, хоть, может быть, и не менее поэтично,
изображает это мифология индусов. Было только великое и страшное одно
(по другим переводам, кажется, оно). Не было ни солнца, ни звезд,
ни дня, ни ночи, ни жизни, ни смерти. Конечно, это поэтическое «преувеличение»:
и солнце было, и звезды, и день, и ночь. Были даже и жизнь и смерть, хоть
они мало друг от друга отличались, ибо живой чудовищный ихтиозавр ничем
не лучше мертвого, - а с точки зрения позднейшего гостя, человека, даже
много хуже. До появления этого гостя все было хаосом и не в греческом мифологическом
смысле, а в нашем нынешнем. Хаос бывал и при человеке, - однако, до него
был только хаос. Он, быть может, еще вернется. Так думали и не одни поэты:
«Но раздвинут мирозданьем, - Хаос мстительный не спит». Так думали и ученые
(и многие религиозные мыслители). В отличие от нас, прежние ученые, не
дожившие до 1945 года, допускали возможность возвращения хаоса лишь в результате
какой-либо космической катастрофы, например, столкновения земли с другой
планетой. Разложив атом, человек показал, что он может добиться такого
же результата и без чужой помощи, своими собственными мозгами и руками.
Несколько тысяч лет тому назад человек на земле еще застал хаос. До философского
понятия случая он естественно тогда еще не возвысился, но все в мире могло
и должно было ему казаться «случайным» (или делом нездешних сил). Сегодня
такое-то явление происходило, на следующий день нет. Не так просто было
заметить, что при этом что-то менялось в условиях явления. Наблюдения накоплялись.
Их было достаточно для первого ограничения роли случая и, разумеется,
недостаточно для того, чтобы признать его вечность при любом ограничении,
- этого не сделали еще и мы. Наблюдения египетских астрономов, наблюдения
Плиния были изумительны; некоторыми из них до сих пор пользуется или еще
недавно пользовалась наука. Древнему человеку понемногу становилось ясно,
что для размышлений над наблюдениями требуются какие-то недоказуемые общие
положения. Появились - говорю здесь только о сфере познавательной - аксиомы
Эвклида (оставим в стороне вопрос об его предшественниках, для нас мало
интересный). Появились первые опытные обобщения, первые открытия в нашем
нынешнем смысле слова. Без аксиом они едва ли были бы возможны. Архимед
ездил в Александрию к Эвклиду учиться. И как Эвклид создал первую научную
аксиоматику, так Архимед, кажется, в древности первый, говорил о законах
природы языком эпохи Возрождения или даже нашим нынешним. Быть может, именно
поэтому его имя две тысячи лет окружено настоящим культом: его убийцы или
вернее их главнокомандующий воздвигли ему памятник. Д'Аламбер считал, что
только он может быть поставлен рядом с Гомером, а совсем недавно Белль
признал его одним из трех величайших математиков в истории (другие два,
по мнению Белля, Ньютон и Гаусс). Заметьте, однако, почти все законы природы,
найденные в древнем мире, оказались неверными... Вы меня опровергали аргументом
о нынешней технике, в основе которой должны же лежать вечные истины. Римляне
строили гигантские акведуки, до сих пор приводящие в изумление людей; тем
не менее они аксиом, законов и философских оснований нынешней механики
никак знать не могли. У них ничего не было, кроме первых и весьма несложных
обобщений. И в течение долгих веков эти обобщения и представляли собой
то, что я называю бессознательной или полусознательной борьбой со случаем,
попытку внести порядок в мировой хаос. Этим обобщениям, законам природы,
со временем придается математическая форма. Еще Лейбниц говорил, что, при
достаточно сложной формуле, можно выразить математически какое угодно явление
природы, хотя бы единичное. Но, разумеется, мысль, желающая упорядочить
хаос, инстинктивно ищет формул наиболее простых. Меня всегда удивляло,
что большим естествоиспытателям не казалась несколько подозрительной огромная
роль цифры 2 в формулах их законов. Это особенно относится к разным отделам
физики (в химии таких законов гораздо меньше). Имею в виду законы типа:
«то-то пропорционально или обратно пропорционально квадрату того-то»...
Что такое цифра два? Второй «сексессор» в ряду Пеано-Ресселя? Почему именно
на ее долю выпала бы такая роль в природе? Почему, вместо цифры 2, не оказалось
бы 1,99 или 2,01, или даже 2,10? Впоследствии так часто и оказывалось.
Можно было бы составить толстую книгу из многочисленных научных исследований,
тщетно старавшихся в течение двух столетий привести опыты в полное согласие
со столь простым, столь элементарным законом Бойля-Мариотта. Но природа
не всегда заботится о простоте и «круглости счета». Она даже о них не заботится
никогда. Вполне точных законов природы нет и теперь. Ученые долго это приписывали
«несовершенству опытов», «неизбежным ошибкам». Однако, не удалось сохранить
в совершенной точности даже закон сохранения материи (а без совершенной
точности очень уменьшается его философская ценность). В полной сохранности
не остались и законы Ньютона. Я понимаю, как это тяжело физикам. Уайтхед
утверждает, что верность Ньютоновых законов движения, в пределах точности
наблюдения, совершенно различна в применении к звездам, молекулам и электронам
(18). Он все же признает их как первое приближение к истине (first
approximation) и для уравнений инфрамикроскопического мира. Книги Уайтхеда
одно из последних слов в области математической философии. Но, быть может,
физики самого последнего поколения под этим его признанием и не
подписались бы.
Л. - Один из самых последних исследователей
именно утверждает, что теория Эйнштейна стремится не к уничтожению Ньютоновской
механики, а к ее поглощению, оставляя за ней ценность истины в первом приближении
(19).
А. - Если это и верно, каково же считать «первым
приближением» то, что в течение двух столетий признавалось непоколебимой
основой точных наук и идеалом каждой из них?
Л. - Сам Ньютон этого не думал. Эйнштейн как-то
отметил, что Ньютон «лучше знал слабые стороны своего «здания идей», чем
следующие поколения ученых» (20). И мне кажется, что то же самое
можно сказать о самом Эйнштейне.
А. - Я этого не думаю. Прочтя три раза его
последнюю, тоже очень нашумевшую работу, я, просто по недостаточности познаний,
не понял ее математического аппарата. Если не ошибаюсь, эту участь со мной
разделяют люди, имеющие неизмеримо большие, чем я, познания, вплоть до
знаменитых математиков и физиков. Могу судить только о философской стороне
основной идеи. Скажу и тут, она a priori подозрительна по своей монистической
простоте. Сам Эйнштейн называет свои четыре заключительных уравнения «необычайно
простой системой» (21). В начале же этой работы он говорит, что,
вследствие математических трудностей, еще не нашел практического пути для
сопоставления результатов своей теории с данными опыта (22). Допустим,
что он практический путь найдет. Допустим даже, что опыт его выводы подтвердит.
Я почти не сомневаюсь, что это наткнется на «дано третье». Нельзя, думаю,
и стараться дать закон, объединяющий разнородные силы и явления природы.
Все слишком «монистическое», слишком «простое», слишком «круглое» маловероятно
и искусственно. Земля вращается вокруг солнца в 365 с чем-то суток, - это
a priori нисколько не подозрительно. Но если б астроном далекого прошлого
заявил, что она совершает свой круг ровно в 1.000 или 10.000 суток без
часов и минут, то это у некоторых философов вызвало бы чрезвычайный восторг,
но у людей точного знания должно было бы вызвать и сомнение.
Л. - Однако, в обоих случаях, с «круглостью»
или без «круглости», они не сделали бы вывода, что закон природы был результатом
борьбы со случаем, - взгляд, неизмеримо более «подозрительный». В вашей
мысли я вижу лишь некоторый пережиток окказионализма.
А. - Ваше последнее замечание очень типично.
Вы, как многие, судите по словесным ассоциациям. Слово случай в известном
смысле переводится на французский язык словом «occasion» (в моем смысле
надо переводить hasard). А уж если «occasion», то, значит, и «окказионализм»!
Нет, тут ничего общего нет. Я для своей «системы» готов обойтись и без
ученого «изма», в отличие от немецких профессоров философии: у них есть
свой «изм» в каждом германском университетском городе, благо это
очень удобно запоминается, выгодно для рецензий и для упоминания в учебниках...
Что такое окказионализм? Учение Геулинкса о двух часах для пояснения взаимоотношений
души и тела? Попытка преодолеть трудности некоторых картезианских понятий?
Все это теперь совершенно не интересно. Сущность же Мальбраншевского окказионализма,
по-моему, заключалась в желании перенести причинность из человеческого
круга в круг высший. Многое в мире дает Богу случай (occasion) от причинности
отступать или же заменять временную причинность в действиях человека своей
собственной вечной причинностью. Отдаленный отголосок этого учения
есть в философии «Войны и мира». Меня в «мальбраншизме» интересовала одна
мысль, - та, что мир может оказаться недостойным Бога и перестанет Его
интересовать. Мысль смелая.
Л. - Будто? Мальбранш вообще смелостью никак
не отличался. Он больше всего на свете боялся огорчить Боссюэта, который,
в конце концов, к великой его радости, его признал, хотя раньше на полученной
им, в качестве верноподданнического подношения, книге Мальбранша начертал
свою высочайшую резолюцию: «Красиво. Ново. Ложно». Вдобавок, Мальбранш
был сумасшедший. Ему всю жизнь казалось, что у него на носу повис кусок
баранины.
А. - Если это не было выдумкой его врагов.
Скажем правду: вы, разумеется, как теперь почти все, открещиваетесь от
позитивизма и еще больше от «Фогта, Бюхнера и Молешотта» (ведь для обозначения
грубого материализма почему-то всегда называют именно этих популяризаторов
из десятка других таких же). В этом вы совершенно правы. Тем не менее ваше
презрение к Мальбраншу как-то, корнями или каким-либо залежавшимся корешком,
уходит к позитивистическому, а может быть, и материалистическому началу,
все же кроющемуся в уме громадного большинства естествоиспытателей. Мальбраншу
можно многое простить и за тонкость многих его страниц, и за его культ
Декарта и особенно за его литературный талант: ведь порою на нем отдыхаешь
душой после долгого изучения немецких философов, начиная с Лейбница...
Л. - Простите отступление в сторону, но я не
могу согласиться и с общим местом о тяжеловесности немецких философских
книг. Германские философы придерживались мнения, что «элегантность надо
предоставить портным», - это изречение приписывают Эйнштейну, но на самом
деле его автор Людвиг Больцман. Философия не фельетон.
А. - Разумеется. И я был бы крайне огорчен,
если б она пошла на какие-либо уступки фельетону. «Элегантность» ей нисколько
не нужна, хотя, по случайному совпадению, быть может, самыми глубокими
философами были именно те, которые и писали ясно, хорошо, «блистательно».
Литературный талант никак не повредил Платону, св. Августину, Декарту,
Паскалю, Шопенгауеру, из новых - Ницше, Соловьеву, Бергсону, Файхингеру,
Франку. Впрочем, я говорил преимущественно о немецких профессорах,
да и тут ничего не обобщаю. У самого Гегеля есть страницы, замечательные
и в чисто-литературном отношении. Возвращаясь к предмету, скажу, что «измы»
есть вещь предательская. Так, например, по сходной словесной ассоциации
вы могли бы назвать мои мысли близкими и к пробабилизму. Я и это должен
был бы отрицать.
Л. - И напрасно. Поскольку вы идее случая и,
следовательно, вероятности отводите в своих мыслях столь важное место,
я имею право хоть до некоторой степени связывать вас с пробабилизмом не
только по словесным ассоциациям. Ведь его создатель Карнеад может считаться
в философском отношении предтечей теории вероятностей. Его, в отличие от
Мальбранша, я ставлю очень высоко. Не думаю, чтобы философия по настоящему
ответила на тот десяток его страниц, которые удалось восстановить историкам.
А. - Очень хорошо, что вы его назвали. Правда,
предтечей теории вероятностей его можно назвать лишь с оговоркой: все-таки
без математики эта теория висела бы в воздухе... Я рад, что вы не боитесь
«отступлений в сторону»: их у нас было и будет очень много. Но если я кратко
коснусь истории теории вероятностей и еще более кратко поставлю
ее в связь с личностью ее трех основоположников, Карнеада (повторяю, с
оговоркой), Паскаля и Фермата, то тут и отвлечения в сторону не будет.
Люди были совершенно разные, разные по складу ума, по душевному настроению,
по взглядам, по всему. Тем не менее в чем-то с теорией связанном, с какими-то
из нее отдаленными выводами, они сошлись, - это обстоятельство само по
себе имеет значение. Карнеад пошел дальше всех. Заметьте, самое слово «вероятность»
встречается у него не часто, кажется, не более четырех раз во всем, что
от него осталось (или, что ему приписывается). Но свой метод он применяет
ко всему, ни перед чем не останавливаясь. Вера в богов? «Я с верой
в богов не борюсь, а только считаю несостоятельными принятые методы ее
доказательства». На самом деле он в пользу «вероятности» существования
богов не приводит никаких доказательств, а в пользу «невероятности» очень
много. Он отрицает существование истины в геометрии, при чем ее не отделяет
от литературы и музыки (23). Его страница о политических формах
правления, о тирании, олигархии и демократии состоит из жестокой и одинаковой
над всеми насмешки (24). Карнеад был первый нигилист в истории мысли.
По словам Цицерона, он, при своем огромном ораторском таланте, мог доказать,
что белое черно, а черное бело. Кто-то другой рассказывает анекдот: приехав
с дипломатической миссией из Греции в Рим, Карнеад в блестящей лекции произнес
похвалу справедливости. Но на следующий же день, в другой блестящей лекции,
он доказал, что справедливость самое отвратительное из явлений. Обе лекции
имели огромный успех. Цицерон, старый адвокат и политический делец, по-видимому,
испытывал нечто вроде профессиональной зависти. Разумеется, Карнеад был
циником не в древнем, а в нынешнем смысле этого слова. Паскаль - прямая
противоположность, о нем распространяться не приходится. И наконец, Фермат,
человек промежуточного типа, еще, к сожалению, мало изученный, хотя по
гениальности близкий к Леонардо да Винчи...
Л. - Не слишком ли сильно сказано?
А. - Не думаю. Хорошо ли вы помните его биографию?
Л. - Я не вижу, какое отношение может иметь
к делу биография ученого.
А. - Только отдаленное, в том смысле, в каком
Гельвеций говорил, что гений шедевр случая (25). Большой, удивительный
сюжет Фермат мог бы дать для романа, если б его жизнь была все-таки немного
лучше известна. Этот сын лавочника сделал головокружительную карьеру. Он
считался одним из самых лучших и беспристрастных судей Франции. Вероятно,
он мог бы стать первым министром короля, ибо был умнее и ученее всех министров
вместе взятых, а Людовик XIV охотно назначал на самые высокие посты людей
невысокого происхождения и даже предпочитал их аристократам, к крайнему
негодованию этих последних и особенно герцога Сен-Симона («неуклонная линия
прогресса» шла так хорошо, что столетием позднее, при Людовике XVI,
накануне революции, человек, не имевший четырех поколений дворянства, не
мог получить даже лейтенантского чина, тогда как в 17-ом веке Катина, отнюдь
не знатный человек, был главнокомандующим и маршалом Франции). Но Фермат
не был честолюбив. По должности он был занят почти целый день. Об его судебно-административной
работе почти ничего неизвестно. Из одного его письма можно заключить, что
он был человек справедливый и добрый (26). В свободное время он
писал стихи на французском, латинском и испанском языках. В его некрологе,
помещенном в «Journal des Scavans» в феврале 1665 года, сообщается, что
писал он их «с такой элегантностью, как если бы жил во времена Августа
или провел большую часть своей жизни при французском и мадридском дворах»
(27), - автор некролога, очевидно, думал, что придворная жизнь очень
способствует развитию поэтического таланта. Фермат был также знатоком древности
и разъяснил немало темных мест в произведениях писателей классического
мира, - это он делал только по просьбе друзей. И, наконец, немного занимался
он и математикой. Своих математических работ он почти никогда не печатал,
- поместил лишь одну без подписи в приложении к математической книге другого
ученого, Лалуэра. Обычно же излагал свои математические изыскания только
в письмах к компетентным друзьям. Они читали и изумлялись. Паскаль считал
его «первый человеком на земле» и говорил, что сам он, как математик, в
подметки не годится Фермату. Очень высокого мнения об его математическом
даре держался и Декарт, хотя они недолюбливали друг друга, особенно вначале,
и порою в геометрии расходились взглядами. Теперь всеми признается, что
Фермат был одним из величайших математиков в истории. Белль называет его
«королем дилетантов» - и добавляет, что, «как чистый математик, Фермат
был по меньшей мере равен Ньютону» (28), - для «дилетанта» похвала
недурная! Что же было бы, если б он дилетантом не был? Лаплас утверждал,
что именно он, а не Ньютон и не Лейбниц, открыл дифференциальное исчисление,
и что он до Декарта наметил основные положения аналитической геометрии.
С этим согласился и Белль. Сам же Фермат не придавал большого значения
своим ученым трудам, да и ученым трудам вообще, - ну, открыл, велика важность!
Но, по-видимому, он был человек не лишенный лукавства. Иногда в письмах
посылал знаменитым ученым математические загадки, - вот как, быть может,
в суде благодушно строил юридические козни состязающимся сторонам: спрашивал
ученых, как бы они решили такой-то вопрос, не сообщая им своего решения.
Одну из его задач разрешил Лейбниц, другую Эйлер, проработавший над ней
семь лет. С третьей же, последней теоремой Фермата (29), вышла странная
история. На полях одной старинной математической книги, «король дилетантов»
записал: «Я нашел поистине замечательное решение этой теоремы, но поля
этой книги недостаточно велики для того, чтобы привести мое доказательство».
Фермат умер в 1665 году, а доказательство не найдено по сей день. Над ним
уже три столетия тщетно ломали и ломают головы знаменитейшие математики,
в том числе Лагранж, Эйлер и Гаусс. В 1908 г. дармштадтский ученый профессор
Пауль Вольфскель завещал сто тысяч марок тому, кто найдет полное доказательство
последней теоремы Фермата (30). Никто до сих пор премии не получил,
а вследствие германской инфляции премия обратилась в ноль... Простите эти
небольшие замечания, не имеющие прямого отношения к нашему спору. Из них
виден образ человека: в политике «centre gauche», в жизни благодушный,
лукавый наблюдатель событий, одинаково чуждый и карнеадовскому цинизму,
и страстной, аскетической, построенной на крайностях натуре Паскаля, с
которым его непонятным образом связывала тесная дружба (психологически
было бы естественнее, если б они друг друга ненавидели). И перед столь
разными людьми стоял один и тот же вопрос о вероятности истины.
Кто-то сказал, что «геометрия случая» появилась в мире по случайности.
Ну, что ж, для создания закона всемирного тяготения потребовалось, чтобы
с дерева упало яблоко, но потребовалось также, чтобы при этом оказался
Ньютон. Так и здесь. Для создания математических теорий вероятности нужно
было, чтобы у шевалье де Мере за игрой в трик-трак произошел какой-то редкостный
казус, но нужно было также, чтобы он был знаком с Паскалем...
Л. - Простите, я не помню: какой шевалье де
Мере и при чем тут еще и он?
А. - Тогда «отступление в сторону». Шевалье
Антуан де Мере был игрок, светский шалопай и очень образованный человек,
недурно писавший мадригалы и разные очерки. Он был хорошо знаком с Паскалем.
Тут уж казалось бы, на заказ трудно было и подобрать человека, который
должен был бы возбуждать такое отвращение у Паскаля, как этот шевалье.
Он был вдобавок влюбленный в себя фат и невероятный хвастун. Семидесяти
лет отроду, узнав, что мадам де Мэнтенон добилась, наконец, своей цели
и выходит замуж за Людовика XIV, он явился к ней и предложил ей свою руку
и сердце: он тоже готов на ней жениться. Воображаю изумление маркизы! Она
все же предпочла выйти замуж за короля. К Паскалю Мере относился благодушно
покровительственно, считал даже себя его учителем в математике. Тем не
менее Паскаль отзывался о нем скорее тепло (31). В один прекрасный
день 1654 года Мере задал Паскалю два вопроса, касающиеся игры в трик-трак.
У великого человека мгновенно возникла мысль о возможности математического
подхода к этим вопросам. Он и нашел новые методы математического мышления,
которыми через полтора века еще восхищался Лаплас. По другой случайности,
вышло так, что своим открытием он поделился с Форматом. Тот чрезвычайно
заинтересовался, послал Паскалю свое решение, сходное и более общее. Таким
образом создалась теория вероятностей. Эти два гениальных или даже сверхгениальных
человека не занимались ее приложением к социальным проблемам. Семнадцатый
век вдобавок был для этого неподходящим временем. Они исходили из случая
в самой маловажной его форме: Паскаль и Фермат игроками не были, да и для
человечества не представляло большого интереса, как будет вестись игра
в трик-трак и можно ли вообще играть «разумно». Учение Паскаля-Формата
осталось почти незамеченным. К нему вернулись по-настоящему в восемнадцатом
столетии. Отчасти вернулись в связи с проблемами страхования людей от смерти.
Но мог быть интерес и гораздо более общий. В начале столетия Николай Бернулли,
член известной династии швейцарских математиков, напечатал работы своего
уже умершего дяди (32). Следуя за Гюйгенсом, Бернулли дал ее первое
основное положение. Теория вероятностей была впервые дана в ее развитой
форме. Нелегко передать впечатление, какое она тогда произвела. Время переменилось,
настал восемнадцатый век, век разума, век оптимизма, век безграничной веры
в знание. Новая наука не дала, но обещала ответ на очень многое. Она отвечала
эпохе и ее wishful thinking: все можно будет со временем подвергнуть математическому
расчету, можно будет предсказывать события, устанавливать коэффициент человеческих
ошибок в науке, в правосудии, в политической жизни, в общественном строительстве,
- можно будет, значит, и вносить соответственные поправки (33).
Были увлечены чуть ли не все математики и философы. Насколько мне известно,
единственное исключение - и странное - составил д'Аламбер. Странное потому,
что, по своей пламенной вере в торжество разума, он должен был бы ухватиться
за новую науку крепче, чем кто-либо другой. Зато столь близкий ему по духу
Кондорсе увлекается больше всех. Он хочет создать «социальную математику».
Впрочем, он допускает, что в общественных науках не все будет доступно
исчислению и предвидению; однако разве дело не обстоит так же с физикой
и с близкими к ней точными науками? И там, и здесь есть «бесконечное множество
предметов, к которым всегда будет закрыт доступ математике; можно на это
себе ответить, что и там, и здесь число вещей к которым математический
анализ может быть применен, столь же безгранично» (34). Труд Кондорсе
характерно и называется: «Опыт применения анализа к вероятности решений,
принимаемым большинством голосов». Уж если можно применять теорию вероятностей
к решениям будущего Учредительного Собрания (книга появилась за четыре
года до революции - и за девять лет до самоубийства автора), то к чему
же собственно ее применять нельзя! Кондорсе не только верил в будущее торжество
разума, но не сомневался в его близости. Теория вероятностей обещала победу
над случаем, - чего же было желать еще! Легко было математику Бертрану
через сто лет после того говорить об очевидных ошибках и наивности Кондорсе
(35). Тогда его труд был принят иначе: он отвечал настроению эпохи.
Менее простительно было такое настроение Лапласу, по крайней мере в ту
пору, когда он писал «Essai philosophique sur les probabilit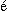 s».
Удивительное дело: в этой книге перечисляются почти все его предшественники
по созданию и по применению теории вероятностей, но имени Кондорсе Лаплас
не произносит, хотя писали они в сущности на одну и ту же тему и почти
в одном и том же духе.
s».
Удивительное дело: в этой книге перечисляются почти все его предшественники
по созданию и по применению теории вероятностей, но имени Кондорсе Лаплас
не произносит, хотя писали они в сущности на одну и ту же тему и почти
в одном и том же духе.
Л. - Это, быть может, по политическим соображениям
было не очень удобно наполеоновскому графу, позднее ставшему королевским
маркизом. Лаплас, при всем своем гении, был лукавый царедворец. В 1810
году он посвятил свой труд «Наполеону Великому», а после крушения Наполеона
довольно бессовестно, хотя и совершенно справедливо, писал: «Взгляните,
в какую бездну несчастий часто погружает народы честолюбие и коварство
их вождей». Мог ли такой человек сочувствовать погибшему жирондисту, одному
из светских святых революции?
А. - Вы видите, что и вам не всегда удается
отвлекаться от личности и биографии ученого. Тут ничего непозволительного
нет, особенно, когда дело идет о Лапласе: он тоже достаточно «красочная»
фигура. Все же ваш подход к нему частью политический, частью моральный.
Я ставлю вопрос иначе. В 1814 году все, случившееся в мире в течение двадцати
пяти лет, могло казаться людям лишь глупой шуткой. На престол казненного
Людовика XVI вступил его брат, и совершенно непонятно было, зачем и во
имя чего погибло несколько миллионов людей. О торжестве разума тогда было
говорить уже довольно неловко, тем более, что, на беду, теория вероятностей
ровно ничего не предсказала. Но во взглядах Лапласа никакой перемены не
произошло. Напомню вам его сто раз с толком и без толку цитировавшуюся
фразу: «Ум, который в известный момент знал бы все действующие в природе
силы и относительное положение составляющих ее существ, - если бы он был
достаточно обширен для того, что бы подвергнуть анализу эти данные, - мог
бы объединить в одной формуле движения самых великих тел и самых легких
атомов: ничто не было бы ему неизвестным, его взору предстало бы будущее,
как прошлое» (36
).
Л. - Что ж, эта мысль сродни учению Декарта
и отвечает «картезианскому состоянию ума».
А. - Ни в какой мере. Лаплас не очень любил
«картезианское состояние ума» и недолюбливал самого Декарта (37).
В истории точных наук, кажется, не было слов более знаменитых, чем приведенная
мною фраза Лапласа. Ею восторгалось несколько поколений ученых, да, может
быть, продолжает кое-кто восторгаться и в нынешнем поколении. Но, кажется,
не было и слов более антифилософских, - даже не грубо-материалистических,
а почти маниакально-механических. Это получше «Бюхнеров и Молешотов», получше
и диалектического материализма, который, по крайней мере в его новейшем
выражении, такого механизма и не проповедует (хотя всем видам материализма
отказываться от фразы Лапласа было бы одинаково трудно). Отмечу и странную
судьбу этой фразы, - как бы завещания 18-го века 19-ому в истории точных
наук. Ее считали откровением, но следовать ей в изысканиях было невозможно:
можно было только скорбеть о том, что такой «ум» еще не появился на свет
Божий... Кажется, Н. О. Лосский высказал мысль, что в условиях свободы
диалектический материализм переродился бы в одну из идеалистических систем.
С механизмом лапласовского вида и этого случиться не могло бы. Если бы
по случайности нашлась какая-либо государственная власть, которая сделала
бы с ним то же, что советская власть сделала с историческим материализмом,
т. е. объявила его обязательным ученьем и десятилетьями вдалбливала его
в головы своих граждан, то они задохлись бы в «Лапласизме» еще гораздо
хуже, чем теперь Россия задыхается от советской метафизики. С ним просто
нечего было бы делать и некуда ткнуться, тогда как при помощи методов нынешней
советской философии все-таки можно изучить, например, вопрос об исторической
роли хлопководства в Туркестане. Непонятно, что сказал эти слова именно
Лаплас, видевший вблизи, как происходят большие исторические события. На
его глазах прошла французская революция, он был министром Наполеона, хорошо
его знал и мог бы видеть, определялись ли «движением атомов», могли ли
бы быть «объединены в общую формулу» решения, от которых зависели судьбы
мира. Что ж делать, можно быть гениальным математиком, никак не будучи
философом. Лаплас вдобавок в душе ненавидел и презирал все «метафизическое».
Пуассон, во многом похожий на Лапласа, в частном разговоре однажды сообщил,
что они вдвоем часто проходили по Avenue de l'Observatoire, почему-то всякий
раз, вступая на эту прекраснейшую из улиц, начинали беседу на «метафизические»
темы - и всякий раз, доходя до какого-то дерева в конце улицы, Лаплас неизменно
произносил непристойные слова. Эти два великих математика были настоящими
энтузиастами теории вероятностей; едва ли кто другой больше, чем они, способствовал
ее необычайному развитию. Но думаю, что философская сторона этой теории
была им не очень ясна. Они не видели и того, что исходят из аксиоматики
все-таки произвольной. Через сто лет после них известный физик Липпман
говорил Анри Пуанкаре об основной теореме теории ошибок: «Все в нее верят,
так как экспериментаторы считают ее математической теоремой, а математики
думают, что она экспериментальный факт» (38). Это порою случается
и с общими положениями теории вероятностей. В философском отношении некоторые
из них все-таки недалеко ушли от простой неученой человеческой речи с простыми
неучеными определениями: «верно», «вероятно», «похоже на правду», «сомнительно»,
«ложно», «нелепо».
. - Вы много говорили об определениях случая
и предложили одно, весьма странное. Есть ли у вас заодно и определение
смежного понятия вероятности? Математики его дают. Не знаю, как философы,
в частности те, которые занимались историей математических наук.
А. - Философского определения вероятности
не дают ни те, ни другие. Курно вначале вообще не хотел пользоваться этим
понятием, - так оно неясно (39). В недавнее время прямо или косвенно
возражали против него Анри Пуанкаре и особенно Бертран. Мизес, кстати,
указал (40), что самое слово «вероятность» Гете употреблял не в
том смысле, в котором его употребляют математики. Конечно, семантические
соображения большого значения не имеют. Отмечу попутно, что Курно был не
очень доволен и словом «hasard»: «Оно иностранного происхождения и случайного
ввоза (d'importation accidentelle) и не принадлежит к органическому фонду
языка» (41). Кант говорит: «Вероятностью называется то, что имеет
на своей стороне больше половины уверенности (Gewissheit), дабы быть признано
истинным». Уж лучше тогда пользоваться одними математическими определениями.
А такие понятия теории вероятностей, как «математическая надежда», «моральная
надежда»? Если не ошибаюсь, в русской науке Чебышев первый стал пользоваться
термином «математическое ожидание» (42), который, по крайней
мере, свободен от элемента желательности, присущего слову «надежда». Да
и он свое выражение предлагает в несколько условной форме: «Если мы примем
называть вообще математическим ожиданием» и т. д. Быть может, не слишком
удачно тут и слово «моральный». О «моральной надежде» сам Лаплас говорит,
что она «определяется (se r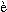 gle)
тысячей обстоятельств, точно расценить которые невозможно» (43).
Спорны в философском отношении и понятия «равновероятный», «равновозможный»,
- «equiprobable», «gleichm
gle)
тысячей обстоятельств, точно расценить которые невозможно» (43).
Спорны в философском отношении и понятия «равновероятный», «равновозможный»,
- «equiprobable», «gleichm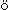 glich».
А можно ли считать философски бесспорным основное положение теории вероятностей,
первый принцип Лапласа: «Вероятность это отношение числа благоприятных
случаев к числу всех случаев возможных»? Пуанкаре считал его сомнительным.
Так же как будто относится к нему и Мизес, который своей теорией «коллективов»
один, после Курно, внес нечто новое в философскую часть теории вероятностей.
Лаплас (да и другие до него и после него) называл это положение неопределенным
словом «принцип». Это, конечно, не теорема, так как она не доказана и недоказуема.
Это и не гипотеза, так как на ней построена вся теория вероятностей, а
трудно было бы построить огромную науку на недоказанной гипотезе. Вы видите,
что это произвольная аксиома, оказавшаяся необычайно плодотворной.
glich».
А можно ли считать философски бесспорным основное положение теории вероятностей,
первый принцип Лапласа: «Вероятность это отношение числа благоприятных
случаев к числу всех случаев возможных»? Пуанкаре считал его сомнительным.
Так же как будто относится к нему и Мизес, который своей теорией «коллективов»
один, после Курно, внес нечто новое в философскую часть теории вероятностей.
Лаплас (да и другие до него и после него) называл это положение неопределенным
словом «принцип». Это, конечно, не теорема, так как она не доказана и недоказуема.
Это и не гипотеза, так как на ней построена вся теория вероятностей, а
трудно было бы построить огромную науку на недоказанной гипотезе. Вы видите,
что это произвольная аксиома, оказавшаяся необычайно плодотворной.
Л. - Это положение самого обыкновенного здравого
смысла. Лаплас и называет теорию вероятностей «здравым смыслом, сведенным
к вычислению», «le bon sens r duit
au calcul» (44).
duit
au calcul» (44).
A. - Здравый смысл говорит также, что через
одну точку можно провести на плоскости только одну линию, параллельную
данной прямой. Быть может, теория вероятностей еще ждет своего Лобачевского.
Первые философские возражения были против нее сделаны еще в 18-ом столетии,
повторяю, д'Аламбером. Его скептические замечания вызвали против него резкие
и даже грубые нападки. «Некоторые большие геометры, - пишет он сам, - признали
мои сомнения заслуживающими внимания. Другие большие геометры нашли их
абсурдными,
- зачем смягчать употребленные ими выражения?» (45). Я не мог установить,
кого д'Аламбер разумел под первыми «большими геометрами». К вторым же принадлежал
Даниель Бернулли, который отозвался об его соображениях даже в еще более
сильных выражениях («ridicule»). К чему сводилась критика д'Аламбера? Он
указал на разницу между математически-возможным и физически-возможным.
Математически совершенно возможно, что, в игре в чет и нечет, чет выпадет
подряд сто или тысячу раз, а нечет не выпадет ни разу. Однако, этого физически
быть не может. Собственно, полагалось бы дать доказательство физической
невозможности этого; д'Аламбер привел лишь аналогию: «Можно дать только
следующую ее причину: не бывает в природе, чтобы эффект был всегда и неизменно
один и тот же, как нет в природе сходства между всеми людьми, между всеми
деревьями». Мы опять тут видим, как опыт или наблюдение легко меняются
местами с математической дедукцией в проблемах теории вероятностей. Примером
могла бы быть и так называемая «Петербургская проблема», чрезвычайно занимавшая
математиков восемнадцатого века. Математически было бы совершенно возможно,
чтобы, при игре Павла с Петром, с такими-то правилами о ставках (не буду
утомлять вас подробностями), Павел выиграл бесконечное число раз и выигранная
им сумма превысила всякую данную величину. Петербургские и иностранные
математики долго бились над этой проблемой; с философской точки зрения
она собственно не разрешена и до сих пор. Один из ученых даже договорился
до такого довода: такая возможность при игре Павла с Петром исключается,
так как состояние Петра, как бы богат он ни был, все же имеет пределы;
он не мог бы проиграть больше того, что у него было! - По свойству человеческой
природы, мы легче воспринимаем не математические, а физическую возможность
и невозможность. Если в рулетке, скажем, номер 22 выпадет пять раз подряд,
то верно ни один игрок не поставит на него в шестой, хотя математически
он может так же легко выпасть снова, как может выпасть какой угодно иной
номер. В романе капитана Марриетта «Простак Питер», во время морского сражения
ядро пробивает дыру в палубе враждебного судна. Находящийся на этом судне
молодой моряк уткнул в эту дыру голову, «ибо, по вычислениям профессора
Иннмана, есть 32,647 с десятыми шансов против того, чтобы в ту же дыру
попало еще второе ядро». Я не читал этого романа, но нашел упоминание о
моряке и ядре в книге доктора Левинсона (46). Конечно, профессор
Иннман никаких таких «вычислений» сделать не мог - и не только потому,
что никогда не существовал. Но не-ученому человеку вы в подобном случае
и не вдолбили бы в голову, что второе ядро может с одинаковой математической
вероятностью угодить и в эту дыру, и в любую другую точку судна. Это шутка
романиста. Возможна, однако, гораздо более серьезная философская критика
теории вероятностей. Вероятное, правдоподобное предполагает существование
верного, правды. Но если правда сама основывается на теории вероятностей,
то получается внутреннее противоречие или заколдованный круг. То, что относится
ко всем научным законам, должно ведь относиться и к закону больших чисел.
«Случай есть нечто стоящее вне законов». Тогда не ищите закона для случая.
«Случай есть псевдоним нашего незнания»? Какая же у незнания может быть
теория? Основной закон Бернулли висел в воздухе до того, как Чебышев дал
ему чисто-математическое доказательство. Из десяти принципов Лапласа, из
которых я привел лишь один первый (основной принцип всей теории), лишь
немногие, никак, например, не третий и четвертый (47) (тоже основной
и чрезвычайно важный), выдержали бы строгий и критический экзамен. Теория
вероятностей могла бы откровенно это признать (но не признала), и это нимало
не уменьшило бы ее огромного значения, как новые геометрии не уменьшили
значения геометрии Эвклида, - она ведь осталась полезнейшей и необходимейшей
из геометрий. Так и теория вероятностей оказывает человечеству очень большие
услуги, хотя и не в тех областях, к которым ее пытались применить Кондорсе,
Лаплас и Пуассон. Очень высока и ее внутренняя ценность, не уступающая
ценности учений Лобачевского и Гильберта. Главная же ее заслуга в том,
что она до сих пор - самая мощная, самая общая и самая успешная попытка
человеческой мысли ограничить роль случая во многих областях познавательного.
Это должен был с особенной ясностью чувствовать Паскаль. Бессмертная книга
«Мыслей» вся насквозь проникнута «метафизическим ужасом» перед мощью Случая
с большой буквы. Это, конечно, не имеет отношения к его соображениям о
задаче де Мере: трик-трак метафизического ужаса вызывать ни у кого не мог.
У людей же 18-го века, вместо метафизики, столь им ненавистной, было просто
глубокое сознание того, что надо бы свести случай к минимуму, надо, чтобы
и войн не было, и чтобы невинных людей не отправляли на казнь. Когда Кондорсе
в последние недели жизни, скрываясь от властей, ожидая каждый час ареста
и казни, писал «Esquisse d'uri tableau historique du progr s
de l'
s
de l' sprit humain», со всей прежней
трогательной и непонятной верой в близкое торжество Разума, он верно и
думать забыл о своей книге по теории вероятностей. Но если бы о ней вспомнил,
то, конечно, пришел бы к выводу, что оба эти его труда, столь несходные
по форме, исходили из одних и тех же душевных настроений и служили одной
и той же цели. От этой веры 18-го века наука, конечно, отошла. Она и в
детерминизме теперь уверена не очень твердо.
sprit humain», со всей прежней
трогательной и непонятной верой в близкое торжество Разума, он верно и
думать забыл о своей книге по теории вероятностей. Но если бы о ней вспомнил,
то, конечно, пришел бы к выводу, что оба эти его труда, столь несходные
по форме, исходили из одних и тех же душевных настроений и служили одной
и той же цели. От этой веры 18-го века наука, конечно, отошла. Она и в
детерминизме теперь уверена не очень твердо.
Л. - Если б наука отказалась от детерминизма,
то она тем самым вообще покончила бы с собой, и это было бы, разумеется,
наиболее трагическое харакири в истории мысли: при отрицании детерминизма
никакое научное исследование вообще невозможно. Вы, вероятно, здесь имеете
в виду уравнения Гейзенберга? Но с ними просто произошло недоразумение
(48). Вопрос об индетерминации, к которому они имели отношение в
одной частной физико-математической теории, смешали с общим спором о детерминизме
и индетерминизме.
А. - Не уверен, что вы правы: кто, быть может,
смешал, а кто и не смешивал. Принцип Гейзенберга может быть верен или неверен,
причинность может быть «ограниченной» или нет, но к случаю это отношения
не имеет. Я приведу вам, в несколько измененной и «модернизированной» форме,
превосходный пример Курно. Человек Икс выходит из дому на улицу. Он делает
это по известным причинам: скажем, прогулка полезна для его здоровья;
или же он привык уходить в тот час, когда у него убирают дома кабинет;
или же у него назначено в это утро свидание; или ему нужно что-то купить.
Можете прибавить к этим сознательным мотивам еще несколько полусознательных
или подсознательнах, вплоть хотя бы до Фрейдовских. Как бы то ни было,
перед вами тут реальная конкретная цепь причинности. Но наряду с ней, совершенно
независимо от нее, действуют другие сходные цепи. В конце улицы, на которой
живет этот человек, стоит высокий старый дом, по таким-то причинам нуждающийся
в ремонте. Его владелец, по своим соображениям, решается произвести ремонт.
Под крышей на подмостках работает каменщик Игрек. Он работает плохо: стар,
или болен, или устал, или в этот день много выпил. В ту минуту, когда человек
Икс проходит по тротуару мимо этого дома, человек Игрек неумышленно роняет
ему на голову тяжелый кирпич, - его рука со скрюченными от ревматизма пальцами
этого кирпича не удержала. Человек Икс падает мертвый с раздробленной головой.
Во всех этих отдельных цепях причинность действовала без отказа. Но скрещение
цепей было случаем. Можно, конечно, придумать философские «объяснения»:
например, «видно, такова была судьба Икса», - это объяснение ровно ничего
не объясняет, да собственно ничего и не значит. Наука в этом и в других
сходных объяснениях не при чем. Другие примеры Курно гораздо менее убедительны.
Два брата, - говорит он, - служат в одной армии и погибают в одном сражении.
Человеческий ум в этом ничего странного не находит: естественно, что братья
старались держаться близко друг к другу, поэтому они попадали часто в одни
и те же опасные места поля битвы и легко могли погибнуть рядом. Но вот
другое событие. Знаменитые генералы Клебер и Дезэ долго были братьями по
оружию, вместе сражались на Рейне, вместе отправились с Бонапартом в Египет.
Затем Клебер в Египте остался, а Дезэ вернулся в Европу. Но оба они погибают
в
один день и в один час: Клебера в Каире закалывает убийца, а Дезэ под
Маренго убивает австрийская пуля. Третий пример: тоже в один день и один
час умирают далеко друг от друга Джефферсон и Джон Адаме, которые долго
были вождями враждебных партий и один за другим правили Соединенными Штатами.
Эти примеры Курно не только не поясняют идеи случая, но скорее ее затемняют.
Еслиб даже было верно, что Дезэ и Клебер или Адаме и Джефферсон умерли
в один час (разница в минутах во всяком случае была), то
это было бы не более «неестественно», чем, например, то, что Шекспир и
Сервантес оба скончались в 1616 году, или даже чем то, что в одном месяце,
в феврале 1953 года, в Нью-Йорке и в Филадельфии умерли два знавших друг
друга столяра. Цепи причинностей тут даже не скрещиваются. Но огромной
заслугой Курно, разительно сказавшейся в его первом примере, было именно
разъяснение понятия цепей причинности и его применение к идее случая. Другая
его заслуга в том, что он разрушил несостоятельную и даже нелепую концепцию
Боссюэта-Лапласа, согласно которой никакого случая нет. Курно дал случаю
и определение. Оно меня, как вы можете вывести из моего общего взгляда,
удовлетворить не может, но, конечно, оно неизмеримо лучше всех дававшихся
до него и после него. Вот оно: «Мы называем случайными (fortuits) или результатами
случая (hasard) такие события, которые вызываются сочетанием явлений, принадлежащих
к независимым цепям в общем порядке причинностей» (49). По-моему,
в учении Курно есть пять недостатков. Первый заключается в том, что он
не признал полной прерывности общего понятия причинности, - того,
что физики называют le discontinu: или же, пользуясь для иллюстрации (разумеется,
только для иллюстрации) языком современных физиков, я скажу, что он мог
бы ввести и не ввел в свое учение идею квант, которую Планк ввел в физику.
Второй недостаток был в его подходе к цепям причинности во времени: для
Курно важен лишь момент единого скрещения двух цепей А и В: тогда возникает
случай. Однако цепь А имеет свою историю и до, и после момента скрещения
с В. На протяжении этой истории цепь А скрещивалась с другими цепями С,
Д, Е, и эти цепи оказываются вовлеченными в соотношение с цепью В. В применении
к нашему примеру предположим, что раздавленный камнем человек Икс был богачом
и имел завещание, по которому его состояние отходило к его молодой жене.
Оставшись неожиданно вдовой, она через год или через десять лет выходит
замуж за бедного человека Дзет, жизнь которого таким образом меняется в
прямой зависимости от скрещения цепей А и В, т. е. от несчастного конца
человека Икс. Человек Дзет следовательно вовлекается в цепь причинности
до того совершенно чуждую ему: он, быть может, отроду не знал и не видел
человека Икс.
Л. - По-моему, тут противоречие. Можно говорить
либо о первом «недостатке», либо о втором. Выходит как будто, что у вас
причинность то прерывна, то беспрерывна.
А. - Тут противоречия нет, ибо цепь беспрестанно
перескакивает из одной плоскости в другую... Винсент Шин где-то говорит:
«у каждого из нас есть две жизни: та, которая есть, и та, которая могла
быть». Не могу с этим согласиться: у каждого из нас есть подлинная жизнь
и тысяча других возможных... Третий, уже иного порядка, недостаток
учения Курно заключается в принимаемом и им принципиальном различии между
явлениями малыми и глубокими. На самом деле никакого принципиального различия
тут нет: вторые интеграл первых. Часто, например, теперь различают так
называемую «малую историю», la petite histoire, от истории «настоящей»
или «большой». И здесь нет ни малейшего принципиального различия. Четвертый
недостаток Курно разделяет со всеми классиками теории вероятностей. Он
не видел, что в основе этой теории лежат произвольные аксиомы. Правда,
он писал до революции, произведенной в геометрии Гильбертом, и мог не знать
о другой, гораздо более ранней революции, произведенной Лобачевским. И,
наконец, пятый недостаток, тоже общий у него, по крайней мере, с Кондорсе,
Лапласом и Пуассоном (никак не с д'Аламбером): он верил в возможность применения
теории вероятностей к целому ряду научных «дисциплин», в которых ей решительно
нечего делать. Курно родился в 1801 году, но, по общему складу своего ума,
он все-таки еще был человеком 18-го столетия со всеми его иллюзиями.
Л. - Вы этих иллюзий не разделяете. К каким
же научным дисциплинам вы считаете эту теорию неприложимой?
А. - Я считаю ее неприложимой именно к тому,
к чему ее прилагали Кондорсе, Лаплас, Пуассон и столь многие другие. Возьмите
любой современный курс этой науки, - вы увидите, что в первой части даются
ее общие положения с разными иллюстрациями, в частности с неизменным в
течение почти трех столетий, очень полезным, но немного надоевшим примером
шаров и орла и решетки; затем начинаются главы о применениях в разных науках,
в разных кругах явлений: теория вероятностей в физике, в химии, метеорологии,
в климатологии, в биологии, в статистике, в страховом деле, в социологии,
в истории, в свидетельских показаниях, в судебных решениях, в парламентских
голосованиях и т. д., вплоть до явлений сомнамбулизма (о которых есть что-то
не совсем мне понятное у самого Лапласа). Так, в старых учебниках по этике,
сначала дается чистая этика, излагаются ее обоснования, ее история, а затем
начинаются главы об этике в личной жизни, в политике, в семье, в браке,
в отношении к жене, в педагогии и т. п. Едва ли нужно говорить, что некоторые
применения теории вероятностей не только совершенно законны, но и дали
превосходные, ценнейшие результаты. Могут быть и еще новые, тоже совершенно
законные и даже обязательные, ее приложения. Думаю например, что подготовка
войны может и будет все в большей мере основываться на теории вероятностей.
Да так собственно было и в прежние времена, только тогда хорошие военные
министры руководились ею бессознательно, быть может, никогда о ней и не
слышав (до Паскаля и Фермата теории вероятностей не было, но хорошие военные
министры были). При создавании вооруженных сил страны можно до некоторой
степени исходить из соображений вероятности, особенно в подсчете того,
чем располагает и будет располагать противник. Да и тут возможны полные
сюрпризы. В 1939 году ни один человек на свете об атомной бомбе не думал.
Чем больше места занимает в данном круге явлений вопрос о вероятности причины,
тем труднее в ней работать с теорией вероятностей. Чем меньше данный круг
явлений насыщен числами, тем меньше эта наука к нему приложима. К биржевым
спекуляциям она поэтому приложима лучше, чем ко многому другому. Но если
бы, скажем, Бернулли, пользуясь всеми им найденными секретами теории вероятностей,
играл на бирже, он наверное потерял бы состояние, ибо, по самому складу
своего ума, едва ли мог разбираться в «вероятности причин», экономических,
политических, психологических, действовавших в Европе в его время. Любой
биржевик наверное понимал их много лучше, - хотя и биржевики не большие
знатоки политической экономии, международной политики и массовой психологии.
Лаплас прилагал теории вероятностей к свидетельским показаниям. Каков его
исходный пункт? Свидетель говорит, что в такой-то лотерее, включающей тысячу
номеров, выпал номер 79. «Допустим, - начинает Лаплас свою (очень стройную)
цепь доказательств, - опыт показал, что этот свидетель обманывает один
раз из десяти». По первому общему положению теории вероятностей, вероятность
выпадения одного номера из тысячи равна 1/1000, и т. д. - отсылаю к его
труду. Допустим, что его общие положения неоспоримы. Но каким образом «опыт»
мог бы показать, что один раз из десяти свидетель лжет? Лаплас не обязан
был быть психологом (хотя в жизни он не раз обнаруживал достаточное знание
людей). Однако в психологическом отношении его математическое допущение
абсурд. Барон Мюнхгаузен наверное иногда говорил правду. Сократ наверное
иногда лгал. Обыкновенный человек то говорит правду, то лжет. Это было
и без Толстых, Прустов и Фрейдов, а в свете их психологических находок
это еще много вернее. Пьер Безухов - правдивейший из толстовских героев
и правдивейший из людей; но, когда его арестовывают французы во время пожара
Москвы, он, «сам не зная, как вырвалась у него эта бесцельная ложь», сообщает
им, что спас из огня свою собственную дочь. Какая же тут может быть статистика:
«обманывает один раз из десяти»! И как на такой основе применять теорию
вероятностей?
Л. - Это возможно, так как все выводы теории
вероятностей имеют силу лишь тогда, когда относятся к достаточно большому
числу фактов одного коллектива (употребляю это слово в смысле Мизеса).
А. - Отчасти именно это и лишает их практического
значения. Кондорсе поставил себе вопрос, сколько присяжных нужно для того,
чтобы исключалась возможность судебной ошибки. Но если и принять его расчеты,
то выходит, что для этого нужно колоссальное число присяжных, и следовательно
никакого практического применения идея Кондорсе иметь не может. Борель,
тоже фанатик теории вероятностей, перевел на ее язык заповедь «Люби ближнего
как самого себя». В интерпретации Бореля, которую он считает единственной
разумной, эта заповедь имеет следующую форму: «Рассматривай каждого из
твоих ближних не как свой эквивалент во всяком случае, но как эквивалент
части тебя самого, заключающейся в пределах между нолем и единицей, никогда
не достигающей нижнего предела (ноля), но могущей порою достигнуть высшего
предела (единицы)» (50). Боюсь, что от этой интерпретации не будет
большой пользы ни религии, ни этике, ни теории вероятностей. А как прилагать
эту последнюю теорию к науке исторической? В истории действуют биллионы
биллионов отдельных цепей причинности. Поэтому ее «законы» совершенно недостоверны.
Она истинное царство случая. Мы могли бы взять темой нашей следующей беседы
именно роль случая в истории.
Л. - Этот вопрос не имеет смысла именно с вашей
точки зрения, по крайней мере в той ее форме, которую вам угодно было назвать
«заостренной»: если случай есть «все что происходит во Вселенной», то как
же его выделять из истории?
А. - Я говорил вам о различии между случаем
непосредственным
и случаем отдаленным.
Л. - Этого, по-моему, недостаточно. Но подождем
ваших исторических разъяснений. Что ж, я так и назову «философией случая»
вашу систему мыслей.
А. - Если непременно хотите придумать название.
Но вы при этом выдвинете одно ее слагаемое из трех.
Л. - Зато, вероятно, самое главное.
1. Р. S. Laplace, Essai philosophique
sur les probabilit s, Paris,
1921, vol. I, p. 106.
s, Paris,
1921, vol. I, p. 106.
2. П. Л. Чебышев, О средних величинах,
Сочинения, под редакцией академиков А., А. Маркова и Н. Я. Сонина, С.-Петербург,
1889, т. I, стр. 687.
3. О нем не упоминает ни Кеинс (J.
M. Keynes, A Treatise on probability, London, 1921) ни Пакье (Gustave
du Pasquier, Le Calcul des Probabilit s,
Paris, 1926), ни Башелье (Louis Bachelier, Le Jeu, la Chance et le Hazard,
Paris, 1920), ни Пуанкаре (Henri Poincar
s,
Paris, 1926), ни Башелье (Louis Bachelier, Le Jeu, la Chance et le Hazard,
Paris, 1920), ни Пуанкаре (Henri Poincar ,
Calcul
dei Probabilit
,
Calcul
dei Probabilit s», Paris,
1912). Ничего, к сожалению, не говорит о Чебышеве вообще и Белль в своей
книге «Великие Математики».
s», Paris,
1912). Ничего, к сожалению, не говорит о Чебышеве вообще и Белль в своей
книге «Великие Математики».
4. Е. F. Riedinger, L'id e
du Hasard, Paris, 1907, p. 5.
e
du Hasard, Paris, 1907, p. 5.
5. R. de Montessus, D finition
logique du hasard, Paris, p. 3.
finition
logique du hasard, Paris, p. 3.
6. Adolf Lasson,  ber
den Zufall, Berlin, 1918, p. 20.
ber
den Zufall, Berlin, 1918, p. 20.
7. Bossuet, Discours sur l'histoire
universelle.
8. S. D. Poisson, Recherches sur
la Probabilit des jugements en
mat
des jugements en
mat re criminelle et en matiere
civile, Paris, 1837, pp. 79-80.
re criminelle et en matiere
civile, Paris, 1837, pp. 79-80.
9. Emmanuel Czuber, Wahrscheinlichkeitsrechnung,
Leipzig, 1908, I,
p. 8.
10. Ernst Mach, Erkenntnis und Irrtum,
Leipzig, 1906, p. 251.
11. Kant, Awspr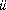 che,
Herausgegeben von Raoul Richter, Lepzig, 1933, p. 22.
che,
Herausgegeben von Raoul Richter, Lepzig, 1933, p. 22.
12. См. об этом Rudolf Eisler, Kant
Lexicon, Berlin, 1930, pp. 620-621.
13. Emmanuel Kant, Critique de la
Raison pure (traduction I. Barni, Revue et corrig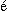 e
par P. Archambault), Paris, s. d., vol. I, p. 244.
e
par P. Archambault), Paris, s. d., vol. I, p. 244.
14. В тяжелом переводе: «Нечто, отсутствие
чего мыслимо».
15. Elie Metchnikoff, Etudes sur
la nature humaine, Essai de philoiophie optimiste, Paris, 1903, p.
336.
16. Emil Borel, Le Hasard, Paris,
1948, p. 231.
17. Richard yon Mises. Wahrscheinlichkeit,
Statistik und Wahrheit, Wien, 1928, p. 181.
18. А. N. Whitehead, An Enquiry
concerning the Principles of Natural knowledge, Cambridge, 1919, p.
18.
19. Е. Baudin, Pr cis
de logique des sciences, Paris, 1938, p. 343.
cis
de logique des sciences, Paris, 1938, p. 343.
20. Albert Einstein, Mein Weltbild,
Amsterdam, 1934, p. 207.
21. Albert Einstein, Generalized
Theory of Gravitation,
приложение к третьему изданию The meaning of Relativity,
Princeton, 1950. p. 146.
22. Там же, стр. 134.
23. Die Nachsokratiker, Собраны
и переведены на немецкий язык Вильгельмом Нестле, lena, 1923, стр. 270.
24. Там же, стр. 266.
25. Цитируется по книге И. Лапшина,
Философия
изобретений и изобретение в философии, Прага, 1924, том I, стр. 15.
26. Oeuvres de Fermat, publi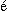 es
par les soins de Paul Tannery et Charles Henry, Paris, 1894, v. II, P.
250.
es
par les soins de Paul Tannery et Charles Henry, Paris, 1894, v. II, P.
250.
27. Перепечатано там же, т. I, стр.
360-61.
28. Е. Т. Bell, Les Grands Mathimaticiens,
Paris, 1950, p. 68.
29. Oeuvres de Fermat, Paris,
1891, t. I, p. 291.
30. В комиссию Wolfskell-Stiftung входили
Элерс, Гильберт, Клейн, Минковский и Рунге (см.. ее Bekanntmachung).
31. Письмо Паскаля к Фермату от 29
июля 1654 года.
32. Jacques Bernoulli, L'Art de
Conjectures. Цитирую по изданию 1801 года (Caen, An X). Николаи Бернулли
сообщает, что его дядя изложил свои мысли впервые в мемуарах Академии Наук
в 1705 году и в «Эфемеридах Парижа» в 1706 году. Автор настоящей книги
этих статей не видел.
33. См. об этом в не очень ценной и
безнадежно устаревшей работе Шарля Гуро, вышедшей более ста лет тому назад.
34. Condorcet, Essai sur l'application
de l'analyse 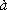 la probabilit
la probabilit des d
des d cisions rendues
cisions rendues  la pluralit
la pluralit des voix, 1785,
p. CLXXXIX.
des voix, 1785,
p. CLXXXIX.
35. J. Bertrand, Colcul des probabilit s,
Paris, 1889, p. 320,
s,
Paris, 1889, p. 320,
36. Laplace, Essai philosophique
sur les probabilit s, Paris,
1921, v. II, p. 3.
s, Paris,
1921, v. II, p. 3.
37. Laplace, Exposition du Syst me
du monde, Oeuvres compl
me
du monde, Oeuvres compl tes,
Paris, 1884, vol. VI, pp. 454-5.
tes,
Paris, 1884, vol. VI, pp. 454-5.
38. Trechet et Halbwachs, Le Cadcul
des Probabilit s, Paris, 1924,
P. IX. He называя имени Липпмана, Пуанкаре сам об этом рассказал в La
Science et l'hypoth
s, Paris, 1924,
P. IX. He называя имени Липпмана, Пуанкаре сам об этом рассказал в La
Science et l'hypoth se.
se.
39. M. A. Cournot, Exposition de
la Th orie des Chance» et Probabilit
orie des Chance» et Probabilit s,
Paris, 1843, p. V.
s,
Paris, 1843, p. V.
40. Richard von Mises, Wahrscheinlichkeit,
Statistik und Wahrheit, Wien, 1928, pp. 10 и 182.
41. M. A. Cournot, Mat rialisme,
Vitalisme, Rationalisme, Paris, 1876, p. 305.
rialisme,
Vitalisme, Rationalisme, Paris, 1876, p. 305.
42. П. А. Чебышев, Сочинения,
Петербург, 1899, т. I, стр. 687.
43. Laplace, Th orie
analytique des Probabilit
orie
analytique des Probabilit s,
Oeuvres compl
s,
Oeuvres compl tes, Paris, 1886,
vol. VII, p. 441.
tes, Paris, 1886,
vol. VII, p. 441.
44. Laplace, Essai philosophique
sur les Probabilit s, v. II,
p. 105.
s, v. II,
p. 105.
45. D'AIambert, Doutes et questions
sur le calcul des Probabilit s.
s.
M lange, de lit
lange, de lit rature,
d'histoire et de philosophie, Amsterdam, 1767,
rature,
d'histoire et de philosophie, Amsterdam, 1767,
vol. V, p. 276.
46. Н. С. Levinson, La Chance,
Paris, 1952.
47. Laplace, Essai philosophiques
sur les Probabilit s, Paris,
1921. v. I, p. 11-13. Этот принцип, согласно которому сложная вероятность
представляет собой произведение простых вероятностей, обычно включается
в теорию, как второй.
s, Paris,
1921. v. I, p. 11-13. Этот принцип, согласно которому сложная вероятность
представляет собой произведение простых вероятностей, обычно включается
в теорию, как второй.
48. Знаменитый физик, профессор Ланжевен,
в давнем разговоре с автором этой книги, сказал «Принцип Гейзенберга не
очень хорошо поняли и физики. Философы же его совершенно не поняли».
49. М. A. Cournot, Exposition de
la th orie des chances et des
probabilit
orie des chances et des
probabilit s, Paris, 1843,
p. 73.
s, Paris, 1843,
p. 73.
50. Emile Borel, Le Hasard,
Paris, 1948, p.195.
<..........................................>