.

К. М. Узбек
(Донецк)

Парадокс как стиль мышления древних

Исследуется проблема парадоксальности мышления античных философов на основе представлений современных мыслителей.

Наука как часть общечеловеческой истории развивается параллельно с развитием человеческого общества. Рассматривая мироздание, мировой космос как что-то хаотическое
и стремясь разобраться в этом хаосе, которым правит некий абстрактный разум (нус),
мыслители древности стремились выработать определенный стиль мышления, установить закономерности явлений, происходящих в окружающем мире. Догреческая наука носила эмпирико-догматический характер. Но она оставила богатый эмпирический материал,
который необходимо было дедуктивно доказать и философски обосновать. Эту великую
роль выполнила древнегреческая наука. Стремясь к установлению всеобщего порядка и нахождению закономерностей мироздания, древнегреческие мыслители выявили
противоречия (парадоксы) и пытались их определенным образом разрешить. Этот парадоксальный (противоречивый) стиль мышления наложил свой отпечаток на
мыслителей всех последующих поколений. Величайшей заслугой этих поколений
мыслителей явилось развитие теоретической науки. «Теоретическое мышление каждой
эпохи... - это исторический продукт, принимающий в различные времена очень различные
формы и вместе с тем очень различное содержание. Следовательно, наука о мышлении, как
и всякая другая наука, есть историческая наука о историческом развитии человеческого мышления» [7, с. 26]. У истоков такого теоретического знания стоял Фалес Милетский
(V I -V вв. дон. э.), глава Милетской школы, математик и философ, один из семи мудрецов Древней Греции.
Но доказательства Фалеса носили предметный характер. Более абстрактные формы
математика получила в пифагорейской школе. Согласно учению Пифагора (580 - 500 гг.
до н. э.), число является сущностью вещей, математические абстракции таинственно
руководят миром, устанавливая в нем определенный порядок. Числа признавались не
просто выражением закономерного порядка, но и сутью материального мира. Учение
Пифагора и его учеников касалось геометрии, теории чисел, астрономии и других наук. Но
более всего они ценили результаты, полученные в теории гармонии. Так, они установили,
что если длины струн относятся как 3:4:6, то они дают наиболее гармоничный аккорд, особое звучание. Большое значение пифагорейцы придавали «золотому сечению». Они считали, что пропорции, установленные с помощью этого сечения, самые совершенные. Но несмотря на
то, что они стремились к установлению гармонии в окружающем мире и в математических выводах, в конечном итоге они пришли к противоречию в результате доказательства
теоремы, устанавливающей зависимость между сторонами прямоугольного треугольника
с² = а²+b² (квадрат гипотенузы равен сумме квадратов катетов - теорема Пифагора). Эта
теорема привела к первому кризису основ математики и всей философской системы пифагорейцев. Как известно, пифагорейцы считали числа сутью вещей. Если существует
число, то существует и вещь, характеризуемая данным числом. Обратного утверждения они
не признавали, т. е. число было первично по отношению к вещи. Но с доказательством
теоремы Пифагора и получением зависимости с² = а²+b² стали появляться числа, отличные
от рациональных, ранее неизвестные, не употребляемые пифагорейцами - иррациональные числа. Возникшие противоречия (в силу того, что еще не были известны иррациональные
числа) привели к кризису основ математики и всей пифагорейской философской системы. Разрешение кризиса оснований математики стало возможным в более позднее время
благодаря работам Евдокса Книдского (408 -355 гг. до н. э.) и его учеников. Математика
перешла с дискретной на континуальную основу. Основой в математике признавалось не
число, а величина, под которой понимался некоторый прямолинейный непрерывно изменяющийся отрезок, который может быть измерен с любой степенью точности с
помощью других отрезков. Разработанный Евдоксом Книдским «метод исчерпывания»
является величайшим творением математики за всю ее историю» [2, с. 197], что привело
к разрешению возникших в результате доказательства теоремы Пифагора противоречий и
первого кризиса ее основ.
Особого внимания заслуживают апории Зенона Элейского (ок. 490 - 430 до н. э.) и противоречивый стиль его мышления, который с помощью парадоксальных доводов
подвергал истины сомнению. Он выдвинул 45 апорий (противоречий), из которых до нас
дошли 9. Его апории направлены против множественности, бесконечности и движения.
Четыре из дошедших до нас именуются апориями движения, это такие как «Ахилес и
черепаха», «Летящая стрела», «Дихотомия», «Стадий». Так, в апории «Ахилес и черепаха» утверждается, что быстроногий Ахилес никогда не догонит черепахи, т. к. пока он пройдет расстояние до черепахи, черепаха за это время пройдет некоторое расстояние, после прохождения им этого нового пути черепаха пройдет новый отрезок пути и т. д. По логике суждений этот процесс бесконечный, т. к. черепаха все время будет опережать Ахилеса и
будет проходить некоторое расстояние, прежде чем Ахилес пройдет предыдущее расстояние.
Но в действительности получается иначе. Ахилес, обладая большей скоростью, должен
обогнать черепаху. Парадокс заключается в логике суждений, не соответствующей реальной действительности.
Если проанализировать суждения Зенона в апории «Дихотомия», то придем к тому, что движение вообще отсутствует. Чтобы пройти отрезок всего пути, необходимо пройти
вначале первую его половину, а чтобы пройти первую половину, необходимо пройти
четверть, потом - восьмую и т.д. до бесконечности. Следовательно, чтобы пройти отрезок определенной длины, необходимо пройти бесконечное множество отрезков, сумма которых
равна

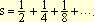
Чтобы пройти весь отрезок, потребовалось бы бесконечное множество отрезков времени,
что практически невозможно. Из этой логики суждений получается, что движение
невозможно. В этом плане также вступают в противоречие действительный факт и логика суждений.
Такая логика суждений настоятельно требовала разработки новых методов перехода от дискретных (прерывных) к континуальным (непрерывным) основам, от конечных множеств
к бесконечным и введения предельного перехода. Аргументы Зенона Элейского также
приводили древнегреческую математику к кризисному состоянию и настоятельно ставили
вопрос о развитии диалектического способа мышления. Математика в частности и наука
вообще в это время развивалась на основе математического атомизма Пифагора и
физического атомизма Левкиппа-Демокрита. В науку настоятельно вводились
диалектические методы и непрерывность (континуальность). Основная мысль, вводимая в
науку Зеноном и Парменидом (учитель Зенона), заключалась в том, что прерывность, множественность и движение - характеристики видимой, чувственно воспринимаемой
картины мира. Но эта картина мира, по их мнению, не является достоверной: истинная
картина мира постигается умозрительно, непосредственно логикой мышления. Попытка
мыслить о множественности мира приводит к противоречию. Если исходить из этой множественной картины мира, то сумма бесконечного множества малых величин приведет
к бесконечно большой, неограниченной величине. Такой постулат является ошибочным в современной математике. На основании предельного перехода, разработанного
французским математиком Опостеном Коши и немецким - Карпом Вейерштрассом, были установлены определенные закономерности в действиях над бесконечно малыми и
бесконечно большими величинами. Но заслуга Зенона Элейского заключается в том, что он поставил эти задачи и установил противоречия.
Задача отображения движения носит противоречивый, диалектический характер. Зенон
и не думал опровергать существование движения, вопрос заключается в том, как выразить
его в логике понятий.
Приведенные примеры показывают, что при изучении любого процесса наблюдается взаимодействие конечного и бесконечного, дискретного и непрерывного. Диалектически развивающиеся процессы необходимо приостановить, изучать в покое, далее необходимо
изучить их диалектически противоречивую взаимосвязь между его элементами, взаимное проникновение противоположностей и выявление тенденции развития этого процесса.
Апории Зенона Элейского не утратили своего значения и в наши дни, т.к. они относятся
к основным законам диалектики и движения, к сложным проблемам оснований математики, связанных с абстракциями актуальной и потенциальной бесконечности.
Диалектика противоречивых суждений проникла повсеместно в жизнь древнегреческого общества. Она проявилась в искусстве ведения спора, в диалогах обыденной жизни, в
судебных процессах, в научных диспутах. Преследовалась одна цель - достижение истины.
Для этого необходимо было оттачивать логику мышления, логическое построение диалога, дискуссии.
Исключительное значение искусству ведения спора придавал Сократ. Он не признавал научных трудов, считал, что невозможно отобразить, выразить в трудах тот диалог,
который может возникнуть в споре, приблизить его к истине. Трудно заранее предвидеть те проблемы, которые могут возникнуть в споре. Сократ утверждал, что диалог - подлинная,
живая и одушевленная речь знающего человека, письменность же - это всего лишь
«подражание диалогу». В письменных сочинениях, полагал Сократ, легче избежать видимых
противоречий, сглаживая острые углы, а в споре, в противоречиях рождается истина. Но это односторонний подход. Невозможно развивать науку без письменности, без аккумуляции
знаний в писаниях, сочинениях. Не записав основных научных выводов, можно потерять
их безвозвратно.
В диалоге Сократ выступал не в роли учителя, а в роли собеседника, более всего он
ценил мастерство задавать вопросы, которые, по его мнению, приводили к рождению
истины в голове собеседника. Этот метод вопросно-ответного диалога, получивший
название метода «майевтики», зачастую ставил собеседника в тупик, и собеседник вступал
в противоречие с самим собой. Сократ подбирал вопросы таким образом, чтобы, когда собеседнику приходилось на них отвечать, он опровергал первоначальное утверждение.
Этот метод «майевтики» или сократовских «ловушек» стал классическим методом в
различных диалогах. В методах ведения спора Сократа сравнивали со скатом, с оводом, в
том смысле, что смущая других, он сам приходит в оцепенение, замешательство. Но,
активизируя таким образом собеседника, он заставляет его поразмыслить, приблизиться к
истине. По этой причине Сократ не оставят письменного научного и литературного
наследия. О его научных исследованиях можно судить по научным публикациям его
учеников, историков, комментаторов, в основном Платона, Ксенофонта, Аристотеля. Но
метод ведения диалога, спора, опровержения, приведения к противоречию, именуемый
методом «майевтики» (повивальной бабки в достижении истины) или сократовской
«ловушки», как впоследствии назвали этот метод, широко использовался мыслителями последующих поколений.
Научный спор, в который Сократ стремился втянуть собеседника, представлял собой мыслительный эксперимент. В начале диалога Сократ старался уточнить основные понятия
и определения, развивая логику мышления и пользуясь индукцией, стремился подвести собеседника к истине.
Такой метод опровержения, т. е. приведения к противоречию по рецепту Зенона
Элейского и Сократа, нашел применение и в математике, как классический метод
доказательства от противного. Для доказательства некоторого положения предпринимается попытка опровергнуть утверждение, формулируемое в теореме. Но если при этом приходим
к нелепости, к противоречию, то утверждение теоремы верно, а опровержение его неверно
[4, с. 62]. Анализируя основные положения и методы построения частных наук, в том числе
и математики, можно вывести следующее заключение: основные понятия, их первоначала,
формы суждений и методы построения разрабатывались в философских школах. Аристотель отмечает, что «... исследовать то, что составляет привходящие свойства сущего как такового
и противоположности его как сущего, - это дело не какой-либо другой науки, а только философии», и далее: «Хотя математик на свой лад и пользуется общими положениями, но
начала математики должна исследовать первая философия» [1, с. 278]. Аристотель
определяет математику и науку о природе (первая философия) как умозрительные науки,
которые предпочтительнее остальных. Но к математике он подходит дифференцированно, рассматривая ее по разделам (арифметика, геометрия, астрономия), каждый из которых занимается определенной сущностью, «а общая математика простирается на все» [1, с. 182].
Следуя Аристотелю, можно отметить, что математики, создавая свои теоретические построения, используют философские выводы, так как методы, разработанные философами, имеют всеобщий характер и применимы ко всем частным наукам. Такие первоначала теоретической математики, как определения, аксиомы, постулаты, определяемые и неопределяемые понятия и др., разрабатывались в диспутах философских школ, и
структурное ее построение - удел не математиков, а философов. Стремясь «обойти» парадоксальные явления, философы строили такие логические конструкции, которые использовались, затем в построениях теоретической математики. Показательным является логико-силлогическая конструкция Аристотеля, которая в дальнейшем использована
была Евклидом в построении знаменитых «Начал». Этот дедуктивный метод стал общепризнанным.
Но следует отметить, что и математика своими методами часто оказывала сильное
воздействие на развитие философской мысли и выводила ее из кризисной ситуации,
например теория пропорций Евдокса Книдского.
Дальнейшее развитие математики продолжалось на дискретной атомистической и континуальной основе. С одной стороны, математический атомизм пифагорейцев и
физический атомизм Левкиппа-Демокрита позволил разрешить многие задачи математики
и естествознания, а с другой - континуальная геометрическая система смело входила в
математику и древнюю науку. Развиваясь параллельно, эти две противоречащие друг другу системы взглядов на окружающий мир привели к созданию дифференциального и
интегрального исчисления и разрешения второго кризиса оснований математики. Корни
этих глубоких противоречий, как видим, были выявлены более двух тысяч лет назад древнегреческими учеными, а их разрешение привело к новому качественному скачку в
научном познании.
Глубокие фундаментальные исследования были проведены древнегреческими исследователями и в области логических построений. Логические парадоксы были
выявлены еще за 2-3 тысячелетия до н. э. Пример - «парадокс лжеца», приписываемый
Евбулиду. «Все критяне - лжецы»,- заявляет критянин. Если он говорит правду и он
критянин, то он, по меньшей мере, один критянин, который говорит правду. Если он
говорит неправду, т. е. не все критяне лжецы, а кто-то говорит правду, то вновь получается парадокс.
Другой парадокс - это парадокс «кучи». Одно зерно не является кучей, а два, три, четыре
и т. д. зерен будут ли представлять кучу? Начиная с какого n+1 количества зерен будем
иметь кучу? В результате таких рассуждений получаем парадоксальное явление, что никогда
не получим «кучи», т.е. множества. Но математически абстрагируясь от материальной действительности и создавая теоретико-множественный аппарат математики, под
множеством принято понимать любую совокупность, в том числе и совокупность,
состоящую из одного, двух элементов и вообще не имеющей ни одного элемента - это
множество, именуемое пустым множеством.
С особой силой парадоксы древних проявились в процессе развития формальной и математической логики, в теории множеств и различных логических исчислений. Они
предстали перед научным миром как парадоксы Рассела, Ришара, Кантора, Бурали-Форти
и других. Бурное развитие новых математических методов, создание теории множеств и арифметизация математического знания, как в фокусе, сконцентрировали все логико-математические противоречия и парадоксы. Эти парадоксы имеют много общего
с парадоксами типа «лжеца», «кучи», апориями Зенона, они направляют мысль
исследователя на построение новых теоретических систем, устраняющих эти противоречия.
Так, Э. Каснер и Д. Ньюмен в статье «Потерянный и найденный парадокс» указывают на
один из источников появления парадоксов: «Обратите внимание на слово «всех» - именно
оно-то и опасно... Когда математик говорит, что какие-то утверждения истинны для
некоторого объекта, то это может быть интересно и наверняка безопасно. Но, когда он
пытается распространить свое утверждение на все объекты, то, хотя это значительно более интересно, но намного опаснее. В переходе от одного ко всему, от специального к Общему математика добивалась своих величайших успехов, но и испытала свои самые серьезные
неудачи, самую важную часть которых составляют логические противоречия» [3, с. 23-24].
Фон Нейман причиной парадоксов теории множеств считал «элементность» множества.
«Это значит, что причиной парадоксов является не существование сверхобширных
множеств, а допущение их в качестве членов других множеств» [6, с. 124].
Д. Гильберт видел устранение парадоксов теории множеств и в любой дедуктивной
теории в полной ее формализации. Он предлагал формализовать не только математические символы и понятия, но и правила вывода. По его мнению, математика должна
превратиться в некоторую совокупность формул, из которых одна переходит в другую по
строго определенным правилам вывода, создав замкнутую аксиоматическую систему. Но
можно ли создать такую аксиоматическую систему, которая бы разрешила все
противоречия? Внутри самой аксиоматической системы появляются неразрешимые
предложения, присоединение которых к предыдущей ведут к расширению этой
аксиоматической системы, а внутри расширенной аксиоматики также возникают
недоказуемые и неопровержимые предложения. Это ведет к построению бесконечной
иерархии аксиоматических систем. Получается, что каждая аксиоматика страдает
дедуктивной неполнотой, она не может доказать все предложения теории.
Австрийский логик К. Гедель в своих теоремах убедительно доказал неполноту
логических систем. Он установил, что в любом логическом исчислении встречаются утверждения, которые невозможно ни опровергнуть, ни доказать с помощью ранее принятой аксиоматической системы. Эти недоказуемые положения либо могут быть проверены
практикой, либо они могут быть доказаны более сильной аксиоматической системой и
включены в предыдущую. Такое расширение аксиоматической системы приводит также к расширению ее дедуктивных возможностей. Эти математические построения еще раз подтвердили противоречивость научного познания.
Следует остановиться еще на одном важном моменте при построении математического
знания, которым является решение задач на построение. Как известно, такого рода задачи решаются с помощью циркуля и линейки. Но с помощью этих средств оказалось
невозможным решить три знаменитые задачи, именуемые «тремя задачами древности» - построение квадрата, равновеликого данному кругу (задача о квадратуре круга), построение
куба, в два раза превышающего объем данного (задача об удвоении объема куба) и деление
угла на три равные части (задача о трисекции угла). Но эти задачи оказались разрешимыми
с помощью других, более сильных аналитических средств. Их значимость в математике и
в науке велика, они оказали сильное воздействие на дальнейшее развитие многих разделов математики. Противоречивость и невозможность разрешения с помощью одних средств и разрешимость их с помощью других, более сильных, явилось мощным толчком в развитии математики, ее оснований и философии. Способность греческого гения к постановке таких противоречивых задач на многие тысячелетия определила направления в развитии
человеческого знания как диалектически противоречивого научного метода.
Невозможность построения всеобъемлющей теории в достижении абсолютной истины, абсолютного истинного знания нашли широкое отражение и в философских системах. Так,
у пифагорейцев это было представлено числовой характеристикой. Следуя пифагорейцам
и Гераклиту Эфесскому, Платон и его последователи поставили в соответствие объектам мироздания «эйдосы» - недостижимые неизменные идеи, а в промежутке между ними - математические фигуры. Философия «Платона - это замечательный образец не ранней и
не средней, но уже зрелой классики, основным содержанием которой и явилась диалектика
идеи и материи как абстрактно - всеобщих категорий», - говорит А. Ф. Лосев [5, с. 63].
Но Аристотель в научном познании признает только то, что в каждом единичном
возможно найти общие принципы. Он придает значение всякой общности, если она
действует, «движется сама и приводит в движение материальные вещи». Для него «важна
не сама идея, но ее текуче-сущностное становление, ее оформляющая сила, ее потенция, ее энергия и порождаемый ею зрительно-смысловой облик вещи, который он называет
эйдосом» [5, с. 69]. Такое стремление постичь непостижимое за счет потенциально -
энергийного и эйдетического приводит его к порождению энтелехии. Это - своего рода непостижимая истина, к которой устремлен познающий человеческий ум (нус). Но
энтелехии Аристотеля, как и эйдосы Платона, до конца непостижимы в познании.
Дальнейшее развитие эти идеи получили в философских системах и Канта - как
непознаваемая «вещь в себе», «абсолют» Г. Гегеля и т. д.
Стремление к разрешению парадоксальных явлений и в настоящее время приводит
научную мысль к построению целых логико-математических конструктивных систем. Это
еще раз убеждает нас в том, что парадоксы древних занимают узловые позиции в научном познании. И попытки их разрешения приводят к дальнейшему развитию научного знания
по различным направлениям. Гениальность древнегреческих ученых заключается в том, что
они с древнейших времен заметили эти неразрешимые противоречия, недостаточность разрешающих средств и поставили их перед всем миром как проблемы классического
суждения, разрешимость которых приводит к различным модификациям.
Подводя итог приведенным суждениям о теоретическом построении научного знания,
следует отметить, что ни одна теория не может быть всеобъемлющей, разрешающей все проблемы, поставленные общечеловеческой практикой и мышлением. Любая теоретическая конструкция имеет ограниченные возможности, но в научном познании укоренился термин «кризис» теории, «тупик» теории. На наш взгляд, не «кризис», не «тупик», а исчерпанные возможности данной теории приводят к парадоксальным суждениям. Такие парадоксы подталкивают сознание ученых к разработке новых научных подходов, к построению новых научных теорий, которые дают возможность обходить кризисные ситуации и новыми теоретическими построениями изучать возникающие проблемы и противоречия.

Библиографические ссылки

1. Аристотель. Метафизика // Сочинения: В 4 т. М., 1976. Т. 1.
2. Бородин А. И., Бугай А. С., Биографический словарь деятелей в области математики.
К., 1979.
3. Каснер Э., Ньюмен Д., Потерянный и найденный парадокс // Математики о математике.
М., 1969.
4. Кессиди Ф. X., Сократ. М., 1976.
5. Лосев А.Ф., История античной философии. М., 1989.
6. Френкель А., Бархиллел И., Основания теории множеств. М., 1966.
7. Энгельс Ф., Диалектика природы. М., 1982.
____________
Журнальная публикация: Узбек К. М., «Парадокс как стиль мішления древних».
-с. 200-210. // Філофсько-антрологічні студії 2001: Спецвипуск. - К.: Стилос; Д.:
РВВ ДНУ, 2001. с-364

_____________________________________________________________________________________________

п